跳到主要内容

一文了解一致性哈希

· 阅读需 12 分钟

前言​

一致性哈希是一种特殊的哈希算法，它的核心思想是在解决分布式环境下，Hash表在动态扩缩容时节点重新映射与大量数据迁移的问题。主要的应用场景是：对于有状态服务等场景，需要根据特定的key路由到相同的目标服务机器上进行处理的场景。

一般情况下我们会使用Hash表的方式，以key-value的方式来做数据的存储。但是，当数据量比较大的情况下，我们会把数据存储到多个节点上，然后通过哈希取模的方式来决定把当前的key存储到哪个节点。但是这种方式有个很明显的问题，就是当存储的节点增加或者减少的时候，原本的映射关系就会发生变化，也就是对于所有的数据需要按照新的节点数量再重新映射一遍，这样就涉及了大量的数据迁移和重新映射的问题，它的代价很大。而一致性哈希算法，就是用来优化这样的动态变化的场景的一种算法。

一致性哈希算法的评判指标：

  • 平衡性：不同key的哈希结果分布均衡，尽可能的均衡地分布到各节点上。
  • 单调性：当有新的节点上线后，系统中原有的key要么还是映射到原来的节点上，要么映射到新加入的节点上，不会出现从一个老节点重新映射到另一个老节点。
  • 分散性：当上游的机器看到不同的下游列表时（在上线时及不稳定的网络中比较常见）, 同一个请求尽量映射到少量的节点中。
  • 服务器负载均衡：负载主要是从服务器的角度来看，指各服务器的负载应该尽量均衡。 一致性哈希算法的关键特征在于： 不要导致全局重新映射， 而是要做增量的重新映射。

实现​

本文将介绍三种一致性哈希算法的实现，代码：demo-projects/consistent-hash at master · straicat/demo-projects

哈希环法​

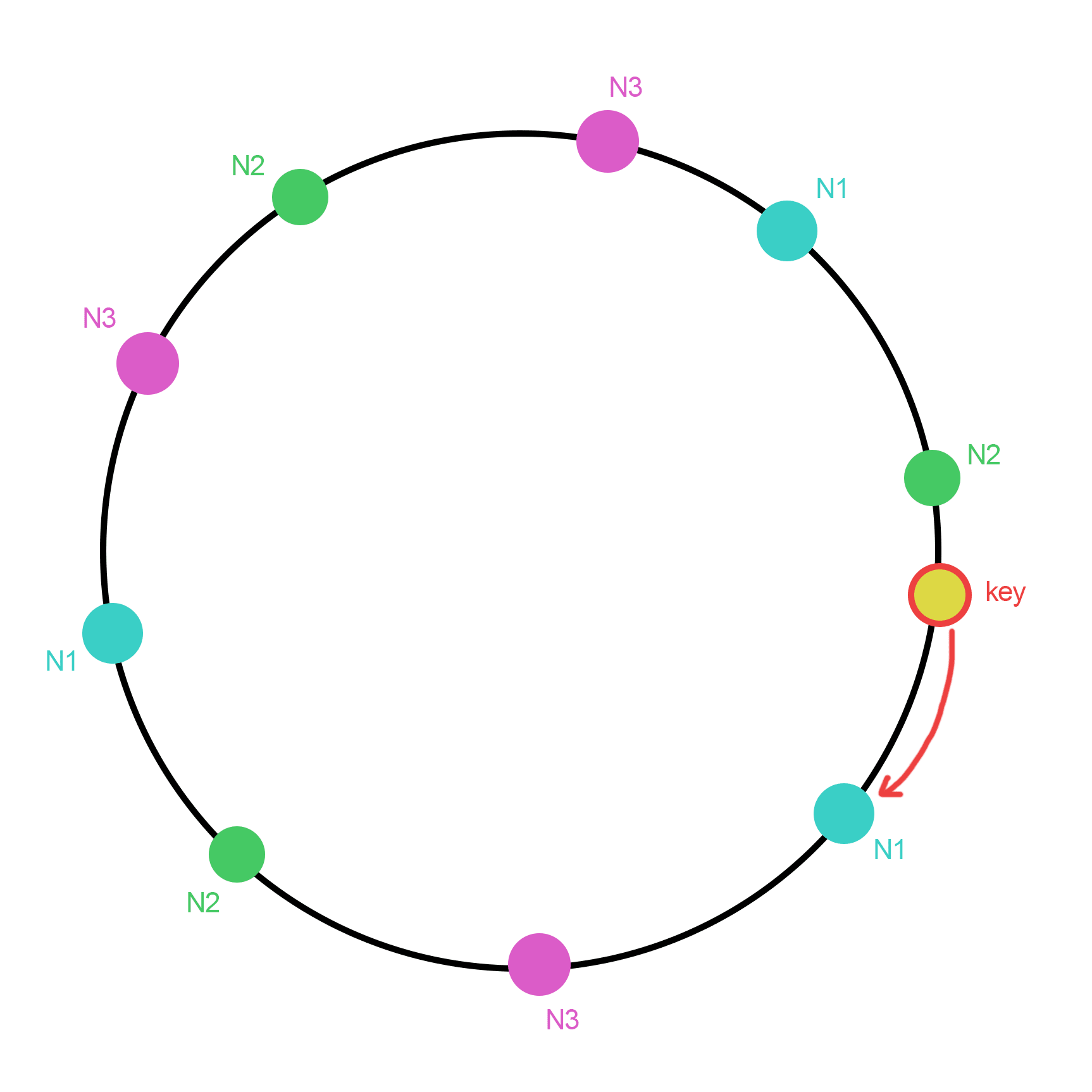
image

哈希环法是最常用、最经典的一致性哈希算法，也叫割环法。这个算法易于理解、应用广泛，实现了最小化的重新映射。

哈希环法的思路是：把节点通过Hash后，映射到一个环上，把数据也通过Hash映射到环上，然后按顺时针方向查找第一个Hash值大于等于数据的Hash值的节点，该节点即为数据所分配到的节点。

哈希环法的映射结果不是很均匀，为了提升均衡性，可以引入虚拟节点（或者叫影子节点）。虚拟节点越多，映射结果的分布越均匀，可以降低真实节点之间的负载差异。虚拟节点不仅提高了结果的均匀性，也能实现加权映射。但是，虚拟节点增加了内存消耗和查找时间。设节点数为n，每个节点有k个虚拟节点，内存消耗：O(kn)O(kn)，查找时间：O(log⁡(kn))O(\log(kn))。

该算法的核心代码：

public Node get(String key) {
    Long hash = hasher.hash(key);
    SortedMap<Long, Node> subMap = vNodes.tailMap(hash);
    if (!subMap.isEmpty()) {
        return subMap.get(subMap.firstKey());
    }
    return vNodes.get(vNodes.firstKey());
}

跳跃一致性哈希​

跳跃一致性哈希 ( Jump Consistent Hash ) 是 Google 于2014年发布的一个极简的、快速的一致性哈希算法：[1406.2294] A Fast, Minimal Memory, Consistent Hash Algorithm

原论文中给出的算法的C++表示：

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
  int64_t b = -1, j = 0;
  while (j < num_buckets) {
    b = j;
    key = key * 2862933555777941757ULL + 1;
    j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
  }
  return b;
}

设n为节点数，k是要映射的key，ch(k,n)ch(k, n)是k映射的结果，也就是映射的节点编号。

  • 当n=1时，因为只有一个节点，所以必然映射到该节点，也就是ch(k,1)=0ch(k,1)=0
  • 当n=2时，此时有两个节点，k映射到这两个节点的概率都是1/2。于是，利用k生成[0,1)的随机数，若该数小于1/2，则k映射到节点1，否则保持在原节点0
  • 当n=3时，此时有三个节点，k映射到这三个节点的概率都是1/3。于是，利用k生成[0,1)的随机数，若该数小于1/3，则k映射到节点2，否则保持在原节点。也就是k有1/3的概率映射到节点2，而有2/3的概率保持在原节点，而原节点有2个，也就是保持在0、1号节点的概率都是1/3。
  • 以此类推，当节点数为n时，利用k生成[0,1)的随机数，若该数小于1/n，则k映射到节点n-1，否则保持在原节点。

需要注意的是，k一旦确定，随机序列就确定了，也就是以k作为随机数种子，之后的循环就是在遍历一个确定的序列，这样k的映射结果是唯一确定的。

但是，上述算法存在一个问题：当n较大时，k映射到新节点的概率很低，也就是在大部分循环中k是保持在原节点。那么，要怎么优化呢？

假设b是k最后一次映射到新节点的节点编号，此时的节点数为b+1。

  • 当增加1个节点时，节点数变为b+2，此时k保持在原节点的概率是(b+1)(b+2)\frac{(b+1)}{(b+2)}
  • 当再增加1个节点时，节点数变为b+3，此时k保持在原节点的概率是(b+2)(b+3)\frac{(b+2)}{(b+3)}
  • 假设节点数变为j+1时，k映射到新节点j。也就是，k最后一次保持在原节点时节点数为j，保持在原节点的概率是(j−1)j\frac{(j-1)}j 那么，k连续保持在原节点直到节点数增加到j+1才映射到新节点j的概率是：

P=b+1b+2∗b+2b+3∗...∗j−1j=b+1jP=\frac{b+1}{b+2}*\frac{b+2}{b+3}*...*\frac{j-1}{j}=\frac{b+1}{j}

如此，上述算法就可以进行优化：当k映射到新节点b后，利用k生成[0,1)的随机数，设节点数为j+1，也就是j是此时的新节点，若该随机数小于(b+1)j\frac{(b+1)}j，那么说明k映射到新节点j。设r为生成的随机数，要满足r<(b+1)jr<\frac{(b+1)}j，那么j<(b+1)rj<\frac{(b+1)}r，也就是j最多移动到(b+1)r\frac{(b+1)}r向下取整。

跳跃一致性哈希算法精妙，在执行速度、内存消耗和映射均匀性上都比经典的哈希环法更好。但是，由于跳跃一致性哈希采用编号来标识节点，所以无法自定义节点编号，并且只能在尾部增删节点。

Maglev一致性哈希​

Maglev一致性哈希算法来自Google在2016年发布的一篇论文：Maglev: A Fast and Reliable Software Network Load Balancer – Google Research ，介绍了网络负载均衡器Maglev所使用的一致性哈希算法。

Maglev一致性哈希的思路如下：

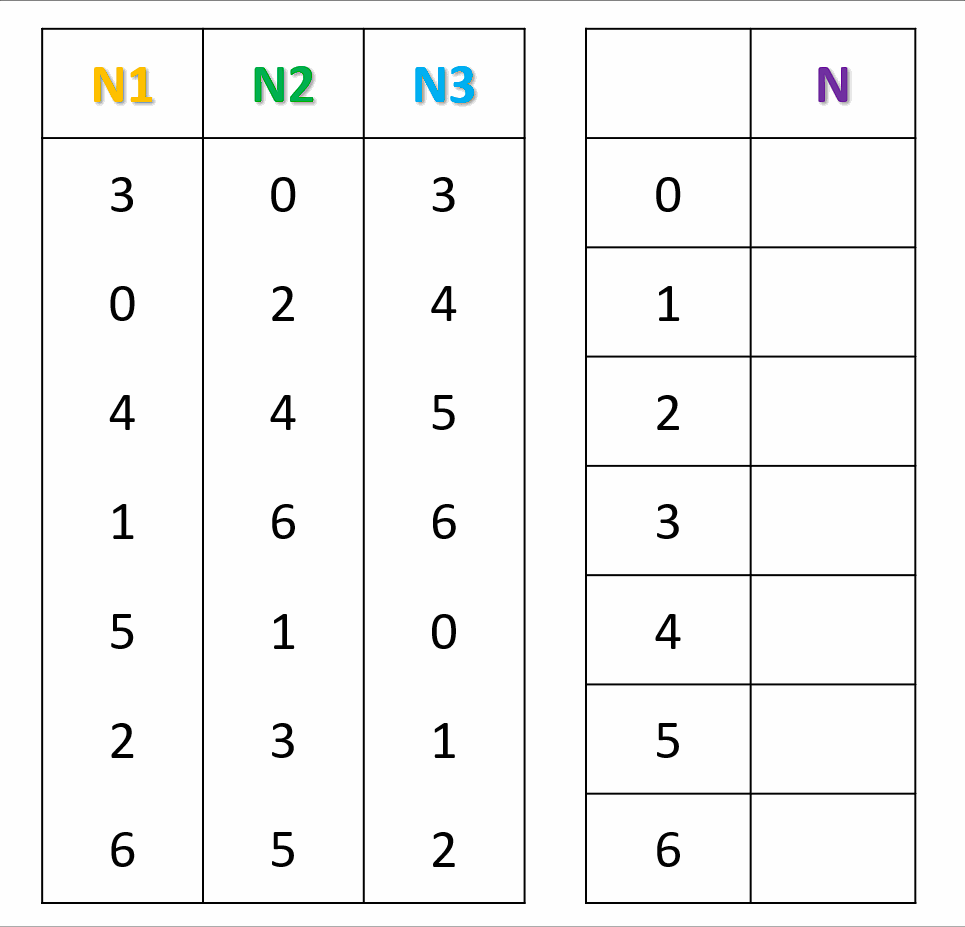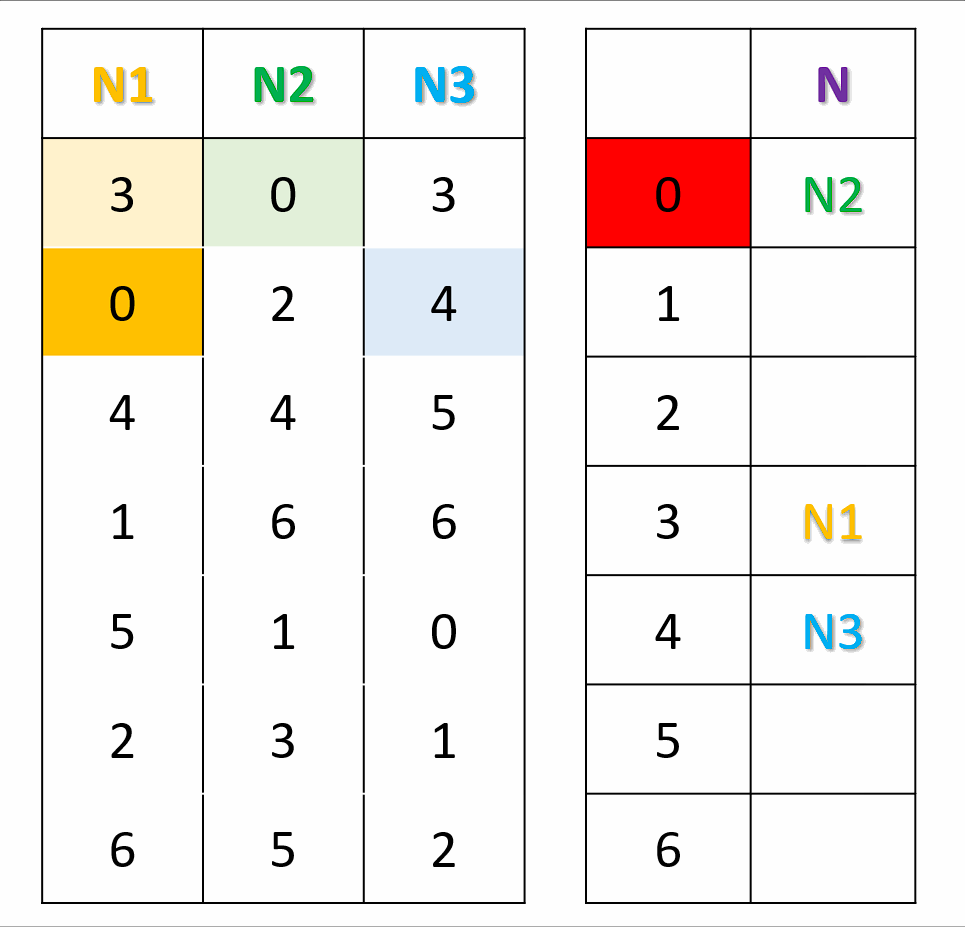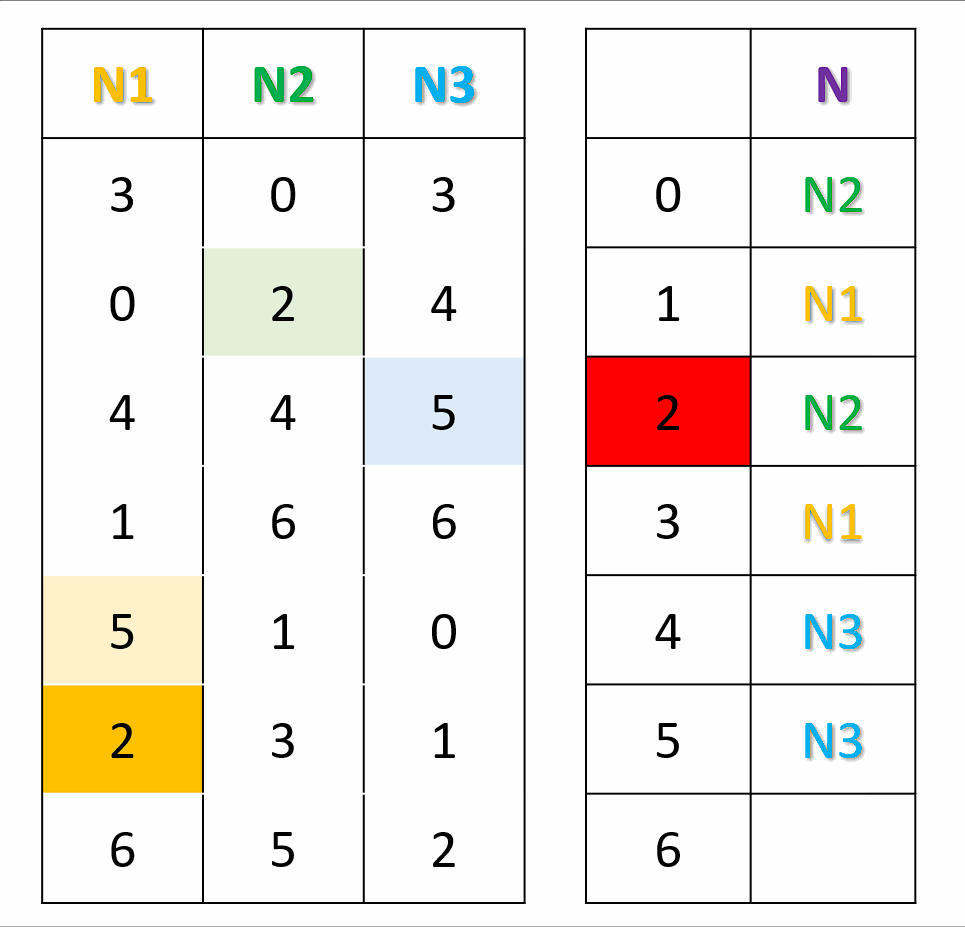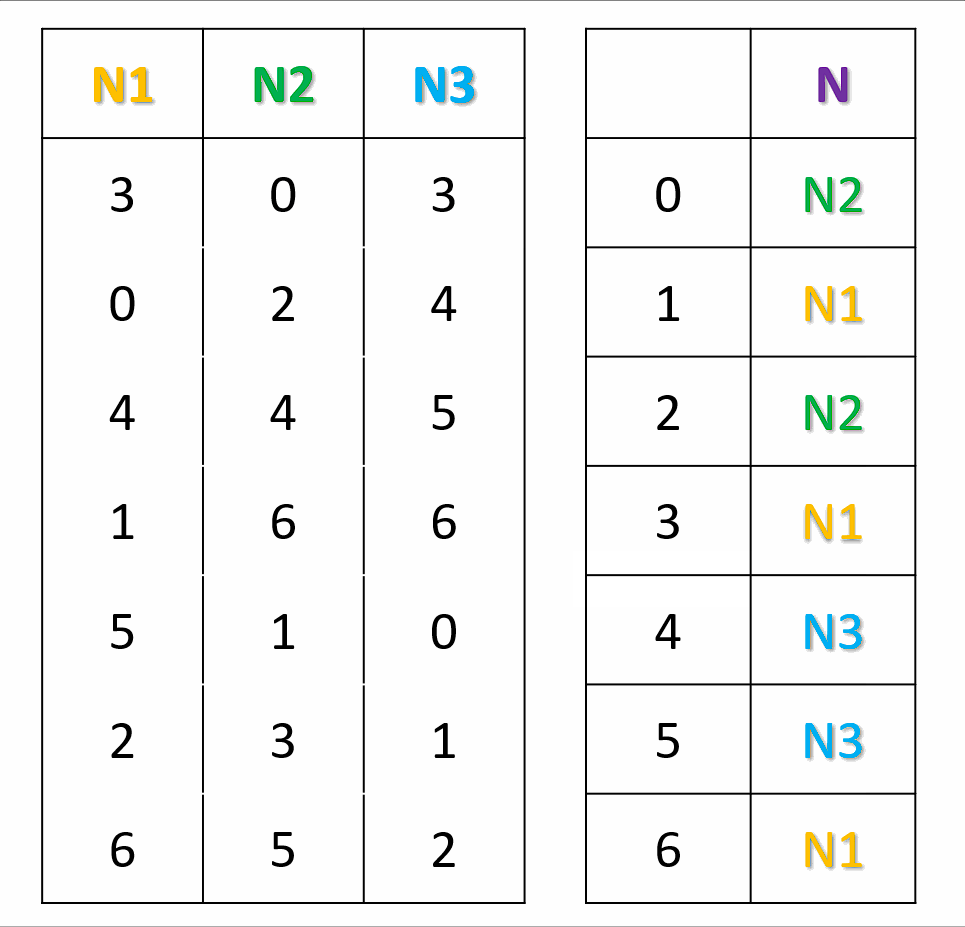
image

对于每一个节点，生成一个偏好序列。按照节点次序，将节点填入结果查找表中编号为偏好序列中的数字的位置。若编号已被占用，则使用偏好序列中的下一个数字再试。按照上面的方法，直到结果查找表填满。在计算key所映射的节点时，将key进行Hash，然后直接在查找表中查找即可。

怎么样生成偏好序列呢？

取两个无关的哈希函数h1h_1和h2h_2，假设节点的名称是x，每个偏好序列的长度是M，先计算offset和skip：

offset=h1(x)%Moffset = h_1(x) \% M

skip=h2(x)%(M−1)+1skip = h_2(x) \% (M - 1) + 1

对于偏好序列中的第j个数，其值为：

permutation[j]=(offset+j∗skip)%Mpermutation[j] = (offset + j * skip) \% M

也可以直接采用一个随机序列来生成偏好序列，只要生成的偏好序列尽量随机、均匀即可。

另外，M必须是个质数，可以减少哈希值的聚集和碰撞，让分布更为均匀。

Maglev一致性哈希生成偏好序列的Java实现：

private void generatePermutation() {
    for (int i = 0; i < N; i++) {
        String name = nodes.get(i).getName();
        long offset = h1(name) % M;
        long skip = h2(name) % (M - 1) + 1;

        int[] row = new int[M];
        for (int j = 0; j < M; j++) {
            row[j] = (int) ((offset + j * skip) % M);
        }
        permutation.add(row);
    }
}

Maglev一致性哈希查找表填表过程Java实现：

private void populate() {
    int[] next = new int[N];
    entry = new int[M];
    for (int j = 0; j < M; j++) {
        entry[j] = -1;
    }
    int n = 0;
    while (true) {
        for (int i = 0; i < N; i++) {
            int c = permutation.get(i)[next[i]];
            while (entry[c] >= 0) {
                next[i]++;
                c = permutation.get(i)[next[i]];
            }
            entry[c] = i;
            next[i]++;
            n++;
            if (n == M) {
                return;
            }
        }
    }
}

参考​