一文了解布隆过滤器
前言
判断某个元素是否在一个集合中在日常开发工作中十分常见,如判断用户是否重复注册、避免伪造不存在的记录导致缓存穿透、判断用户是否参加过某活动等。最直观的做法是使用HashSet,底层使用哈希表,但是哈希表在元素数量很大时需要占用非常大的空间。
布隆过滤器(Bloom Filter)是 1970 年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于判断一个元素一定不在某个集合中,以及一个元素可能在某个集合中,对于存在性它有一定的误判率。它的优点是空间效率和查询时间都远远超过一般的算法。
工作原理
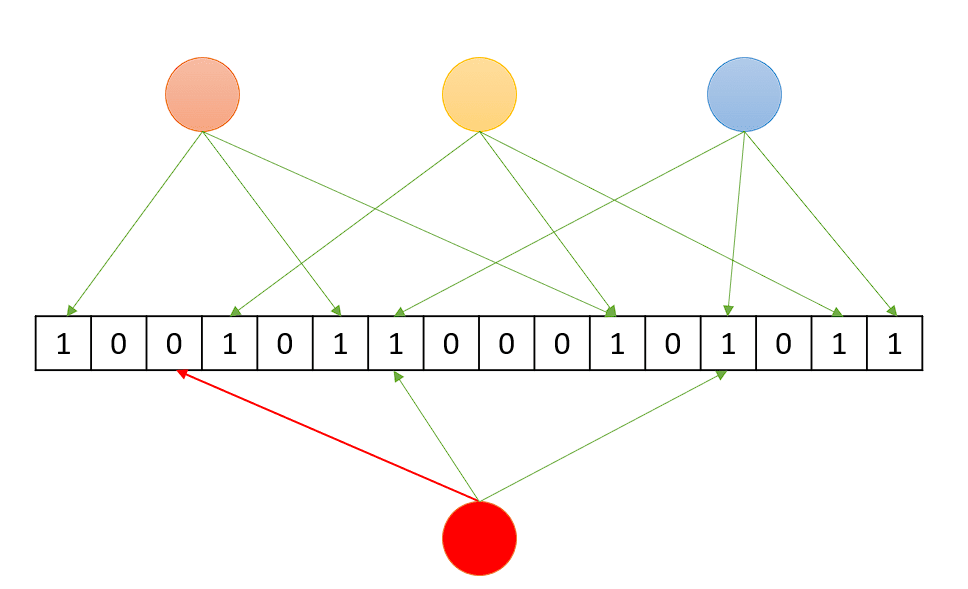
布隆过滤器的工作原理是:
- 当一个元素加入集合时,通过k个哈希函数将该元素映射到bit数组的k个位置,并将这些bit置为1
- 检索时,将检索的元素同样映射到bit数组的k个位置,如果其中存在某个位置的bit不为1,那么检索的元素一定不存在于集合中,否则可能存在。
布隆过滤器的优点是:占用空间极小,且插入与查询的时间复杂度均为常数级别,效率高。
布隆��过滤器的缺点是:判断存在时有一定的误判率;无法删除元素。
定量分析
优化,后面实现用到的优化都要在定量分析中体现。
下面定量分析布隆过滤器的误判率。设:
m:bit数组的长度k:哈希函数的个数n:插入元素的个数p:误判率
假设哈希函数是均匀的,那么每个元素映射到bit数组中每个bit位的概率都是1/m。
插入一个元素时,由于要经过k个哈希函数,所以对于bit数组中某一个bit位,该位置没有置为1的概率是:
插入n个元素后,该位置仍然没有置为1的概率是:
也就是,插入n个元素后,该位置被置为1的概率是:
那么k个位置均被置为1的概率是:
这个概率便是误判率。
由于,所以上式可以近似为:
p可以看成是k的函数,令,考虑关于k的函数:
该函数图像如下:

两边同时取自然对数并求导:
令,即:
令,即,上式可化简为:
故,于是:
此时,布隆过滤器的误判率最低。将此时的k代入误判率的公式中可得:
实现
Java中可以使用BitSet 作为bit数组。布隆过滤器的Java实现:
import com.google.common.hash.Hashing;
import java.nio.charset.StandardCharsets;
import java.util.BitSet;
public class BloomFilter {
private int n, m, k;
private double p;
private BitSet bits;
public BloomFilter(int n, double p) {
this.n = n;
this.p = p;
m = (int) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
k = Math.max(1, (int) ((double) m / n * Math.log(2)));
bits = new BitSet(m);
}
public void add(String key) {
long hash = Hashing.murmur3_128().hashString(key, StandardCharsets.UTF_8).asLong();
int h1 = (int) hash;
int h2 = (int) (hash >>> 32);
for (int i = 1; i <= k; i++) {
int h = h1 + i * h2;
if (h < 0) {
h = ~h;
}
bits.set(h % m);
}
}
public boolean contains(String key) {
long hash = Hashing.murmur3_128().hashString(key, StandardCharsets.UTF_8).asLong();
int h1 = (int) hash;
int h2 = (int) (hash >>> 32);
for (int i = 1; i <= k; i++) {
int h = h1 + i * h2;
if (h < 0) {
h = ~h;
}
if (!bits.get(h % m)) {
return false;
}
}
return true;
}
}
注意:Java中,Math.log是以自然对数,也就是以e为底,而Math.log10才是以10为底的对数。
在论文《Bloom Filters in Probabilistic Verification》中指出:尽管布隆过滤器需要k个哈希函数,但其实可以通过两个哈希值来计算,达到k个哈希函数的效果。
布隆过滤器的参数设置可以使用在线网站Bloom filter calculator 方便进行参数评估。