使用TensorFlow进行线性回归

我们先随机生成一些数据：

import numpy as np

train_X = 20 * np.random.rand(100).astype(np.float32)
train_Y = (30 * train_X + 100 + 10 * np.random.randn(100)).astype(np.float32)

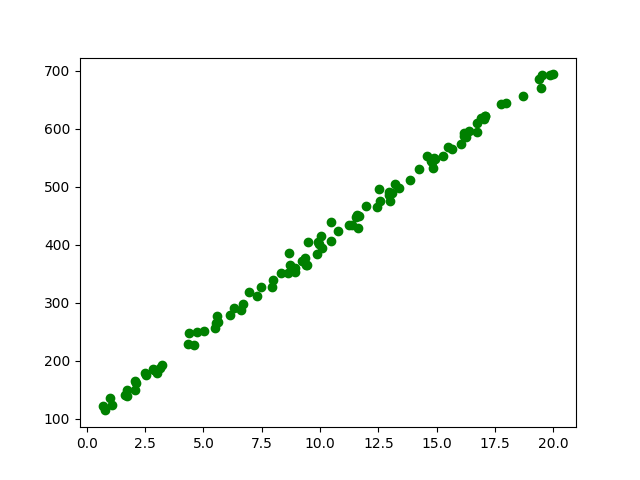
预期拟合的函数为：

$Y = 30 X + 100$

现在我们使用线性回归，假设拟合的函数为：

$y = W x + b$

先给W、b赋初值，然后计算y和实际值的差距，并使用梯度下降算法来减小差距。定义这个差距（损失函数）为：

$C = \frac 1 {2m} \sum _{i=1} ^{m} (Y_i - y_i)^2$

现在使用TensorFlow来完成。

首先定义变量：

import tensorflow as tf

W = tf.Variable(1.0)
b = tf.Variable(0.0)
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
y = tf.add(tf.multiply(W, X), b)
cost = tf.reduce_sum(tf.pow(Y-y, 2))/(2*train_X.shape[0])

W、b是待训练的参数，使用tf.Variable；X、Y接收输入的数据，使用tf.placeholder。

然后开始训练：

init = tf.global_variables_initializer()
train = tf.train.GradientDescentOptimizer(0.2).minimize(cost)

with tf.Session() as sess:
    sess.run(init)
    for i in range(100):
        for tx, ty in zip(train_X, train_Y):
            sess.run(train, feed_dict={X: tx, Y: ty})

        if (i+1) % 10 == 0:
            c = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            print('epoch: %d   cost:%f   y = %f x + %f' % (i + 1, c, sess.run(W), sess.run(b)))

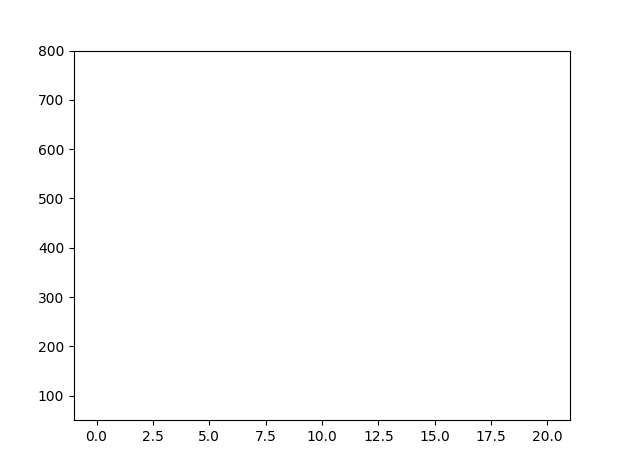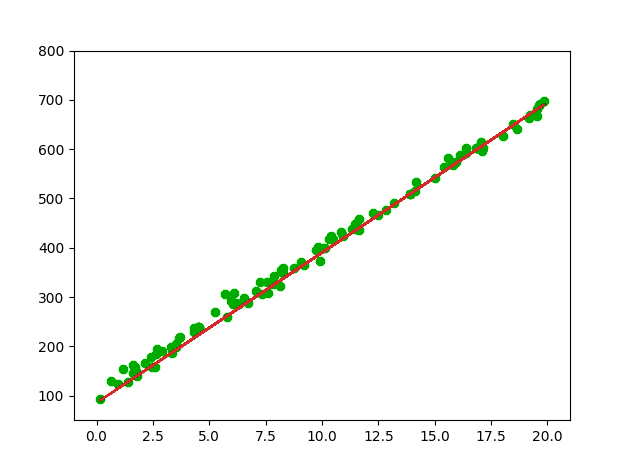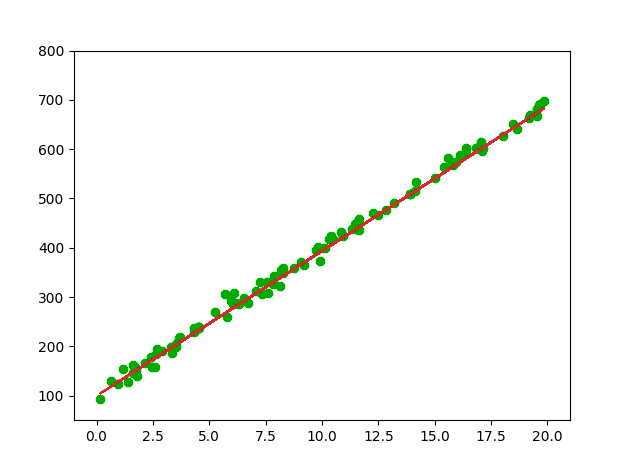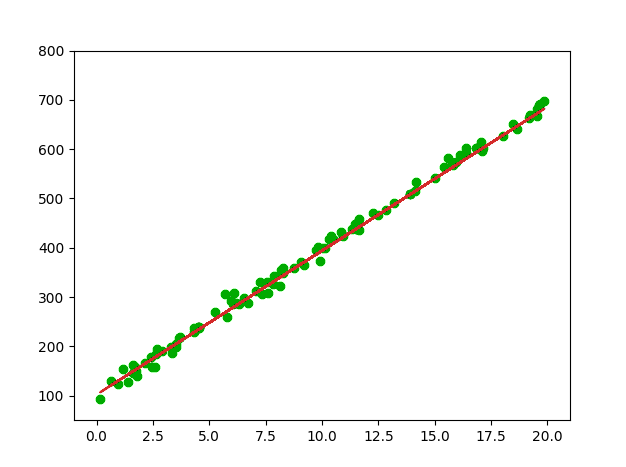
可以看到，拟合的结果还不错。